Calculus: The Mathematical Engine Powering Change and Motion
Calculus, one of the most profound innovations in mathematics, revolutionised how we understand the world by providing tools to model change and motion. Developed in the 17th century by Isaac Newton and Gottfried Wilhelm Leibniz, calculus serves as the foundation of numerous fields, from physics to economics. Its powerful concepts of differentiation and integration allow us to unravel the complexities of natural and artificial systems, making it indispensable both in theoretical studies and practical applications.The Origin and Purpose of Calculus
The invention of calculus was driven by the need to solve problems related to motion and area under curves—issues that traditional geometry struggled with. Isaac Newton initially applied calculus to his laws of motion and gravitation, while Leibniz developed the notation still in use today. Their independent work laid the groundwork for what we now know as differential and integral calculus. The Fundamental Theorem of Calculus ties these two branches together, asserting that differentiation and integration are inverse operations.
Core Concepts and Operations of Calculus
The essence of calculus lies in two central operations:
1. Differentiation: The process of finding the derivative of a function, which represents the rate of change of one quantity with respect to another. Derivatives help in determining instantaneous speed, acceleration, or how one variable changes in relation to another.
Popular Equation:
2. Integration: The reverse process of differentiation, which deals with the accumulation of quantities, such as areas under curves or total distance travelled over time. It is used to compute quantities where data changes continuously.
Popular Equation:
The Fundamental Theorem of Calculus connects these two processes:
Note on Abbreviation: In integrals, stands for the constant of integration, which represents an unknown constant that arises because integration is the reverse of differentiation. When finding indefinite integrals, the function's general form includes this constant.
Calculus in Action: Equations and Applications Across Disciplines
1. Physics and Motion
One of the most famous equations derived from calculus in physics is Newton’s second law of motion:
F = ma
Kinematic Equations derived from calculus describe the motion of objects under uniform acceleration, for example:
2. Economics and Optimisation
In economics, calculus is vital for optimising profit, cost, or production. The marginal cost or marginal revenue is found using derivatives, which indicate how changes in production or pricing affect profit.
Equation for profit maximisation:
3. Population Growth in Biology
The logistic growth model, used to describe population growth with limiting factors, is governed by a differential equation:
Day-to-Day Advantages and Applications of Calculus
Beyond academic and industrial applications, calculus is embedded in many everyday technologies:
GPS and Navigation: Calculating the shortest distance between points on Earth’s surface, known as geodesics, involves calculus. Integrating the velocity of a moving object provides the total distance travelled, enabling accurate navigation.
Weather Forecasting: Meteorologists use calculus to model atmospheric changes. Partial differential equations help predict how pressure, temperature, and wind evolve, making weather predictions more accurate.
Loan Repayment Calculations: Banks use integral calculus to determine how much interest accrues on loans over time. Compound interest calculations involve continuous growth functions, made tractable by calculus.
Visual Representation: Calculus in Motion and Change
Consider the graph below illustrating the relationship between differentiation and integration using the position and velocity of a moving object:
The tangent line at any point represents the object’s instantaneous velocity (rate of change of position), while the area under the curve shows the total distance travelled, calculated via integration.
Interesting Real-World Examples
1. Space Travel: NASA uses calculus to plan spacecraft trajectories. The rocket's position, velocity, and acceleration must be continuously recalculated as it travels through space, subject to varying gravitational forces and atmospheric resistance.
2. Optimising Traffic Flow: Traffic engineers use differential calculus to optimise the timing of traffic lights and manage congestion. By understanding the rate of car arrivals at intersections, they can minimise wait times and fuel consumption.
END NOTE
Calculus is not just a branch of mathematics; it is the key to unlocking the secrets of continuous change in our dynamic world. Whether determining the trajectory of a spacecraft or optimising production in a factory, calculus provides a framework for solving complex problems and modelling real-life situations. Its profound impact spans physics, economics, biology, and beyond, cementing its status as an essential mathematical tool. As we navigate through an increasingly data-driven world, calculus continues to be the engine that drives innovation and progress, quietly shaping the way we live, move, and interact with our environment.





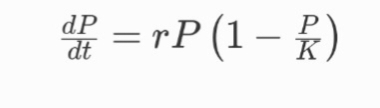










No comments:
Post a Comment